Tutorials | Foreground and Background in Focus
What we're trying to do here is get as much of the foreground and background in focus as possible.
To do this we will utilise a calculation which generates what's called the Hyper-focal Distance. If we focus at that distance we automatically have the maximum depth of field available for that given camera, focal length and aperture. Maximum depth of field is the largest possible distance between two objects that are in focus. For example, rocks on a shoreline through to mountains in the distance.
This technique is quite useful for anyone interested in landscape photography as it allows for both near and far objects to be "acceptably in focus"*.
* By acceptably in focus we mean that it's sharp enough to be acceptable to the viewer.
This short tutorial is based on a post I made at pixalo.com where I spouted, as fact, some nonsense about Hyper-focal Distances and Maximum Depth of Field.
At the time I thought to get Max DOF you simply focused at ∞ (infinity). When you did this you automatically got everything from ∞ to a set distance in focus. I thought this distance was called the Hyper-focal Distance.
Turns out I was talking nonsense. :)
The Right Way
The correct procedure to get maximum depth of field is to calculate the Hyper-focal Distance for your current sensor/film resolution, focal length and aperture. You then focus at that distance. From that point, everything from half the Hyper-focal Distance to ∞ (infinity) will be "acceptably sharp".
There's two problems with this. The first problem is the arithmetic required to calculate the Hyper-focal Distance - it isn't something that lightly trips off the tongue: -
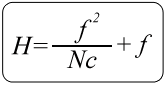
Where: -
H = Hyperfocal Distance- f = Focal Length
- N = F Number (Aperture)
- c = Circle of Confusion Limit (Dependent on your camera and sensor. For APS-C sensors, use 0.018 and for 35mm use 0.029)
Luckily there are tools and charts you can buy/download which make it a lot easier to get the correct Hyper-focal Distance for your current situation. Sadly it's a bit on the clumsy side to have to keep looking up charts distance - although I'd grant you'd probably start to recite these distances in your sleep after using them for a while :)
In any case, whatever the mathematics involved, it's nothing compared to the second problem - actually focusing at the Hyper-focal Distance!
Lets say you're at F/11 and 10mm on a Nikon D50. That would give you a Hyper-focal Distance of 59cm. That means you need to focus at 59cm - something that's particularly difficult to do given the focus scales on today's lenses. For example, lets look at the focus scale of the Sigma 10-20mm f/4-5.6 EX DC HSM lens: -
|
||
| Sigma 10-20mm f/4-5.6 EX DC HSM Focus Scale |
|---|
Notice that the scale is logarithmic (half way between 0.3 and 0.4m is NOT 0.35m). It's highly unlikely that the Hyper-focal Distance you want will be marked on the focus scale, that means you'll have to judge the correct focus position by guesswork, experience or understanding logarithmic scales!
Alternatively you can pull out a measuring tape, stand in front of your camera at what you think is the correct Hyper-focal Distance (measure from near the front of your lens) and take a shot in automatic focus mode. Now switch your camera to manual focus and that "should" be you focused at the Hyper-focal Distance.
One the plus side, if you don't get the focus point correct it may not result in a sin-binned image. Using the 10mm/F11/D50 example above, if you focus at 1m instead of 59cm then objects at ∞ will still be acceptably sharp, it's just the nearer objects that'll go out of focus. To be exact instead of items from 30cm to ∞ being in focus it'll be 37cm to ∞. Not too bad a loss. Note however that the amount of loss will improve with smaller apertures and get worse at longer focal lengths.
The Wrong Way
So to save yourself all this hassle with measuring tapes, maths and stepping into the sea at the correct distance from your camera simply focus to the ∞ mark on your lenses focus scale.
Be aware, however, you will loose some depth of field so if you have an object in frame that you want to be in focus then you will have to do it the right way or move further away from the object.
The table below shows comparisons of the distance for nearest object in focus for a given focal length / aperture when focusing at the Hyper-focal Distance (The Right Way) and focussing at ∞ (The Wrong Way) as well as the difference between the two - I.E. the amount of Depth Of Field you loose by using The Wrong Way :)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Table based on the resolution of a Nikon D50 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
In the above examples I've focussed at ∞ instead of doing it The Right Way. You can see that the results aren't actually that bad. I just need to make a point of doing the proper focussing for some comparisons.
In practice, with my ultra-wide angle lens - especially @ 10mm - it's simply not worth the hassle to do it The Right Way - especially given how crappy the focus scale is on the lens.
p.s. Just so you know, the measurements are taken from the focal plane of the camera. You can tell where that is as there is a marker on the underside of you camera body telling you where the focal plane is. Also, the screw socket for tripods is on that plane too.
Good luck, have fun.
Neil.






